Adaptive Mathematical Morphology with Fuzzy Structuring Element
Mingzhu
Zhanga,
Mengdi Sunb,
Huichao Sunc,
Zhonggui Sund,*
aChongqing
University
of
Posts
and
Telecommunications,
College
of
Computer
Science
and
Technology,
Chongqing,
China
b
Dong'e Nanhu Xingzhi School,Liaocheng,China
c
Shandong Normal University, School of Information
Science and Engineering, Jinan, China
dLiaocheng University, School of Mathematical Sciences, Liaocheng, China
Abstract
As a
well-known nonlinear tool, mathematical morphology (MM) is still active in image
processing. Benefiting from the fixed structuring element (SE),traditional MM
(TMM) gets solid theoretical foundation. However, due to the inherent diversity
of pixels in an image, the rigid SE paradigm is not always practical. As a
result, the development of morphology with adaptive SE, known as adaptive MM
(AMM), has been a significant challenge. In this work, we present a novel
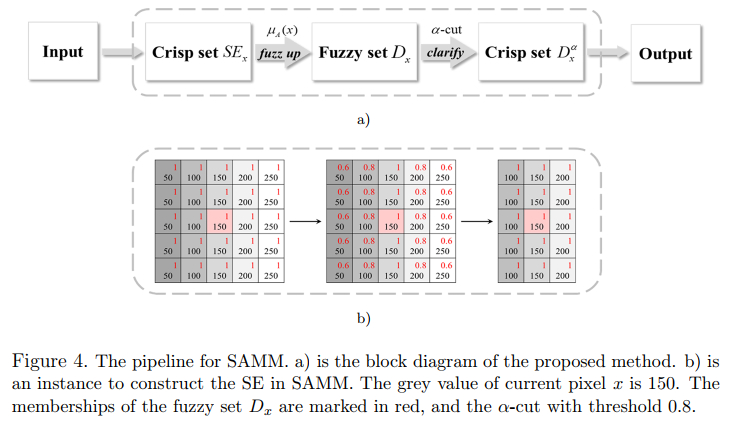
approach for designing adaptive SE using the α-cut of a fuzzy set. By
implementing dilation and erosion operations serially, we obtain an AMM (named
SAMM) that is both adaptive to image content and robust to noise. Additionally,
the operators in SAMM inherit important properties from TMM as much as possible.
We provide theoretical proofs and simulated results to support our conclusion.
Preliminary experiments on edge detection and noise reduction confirm the
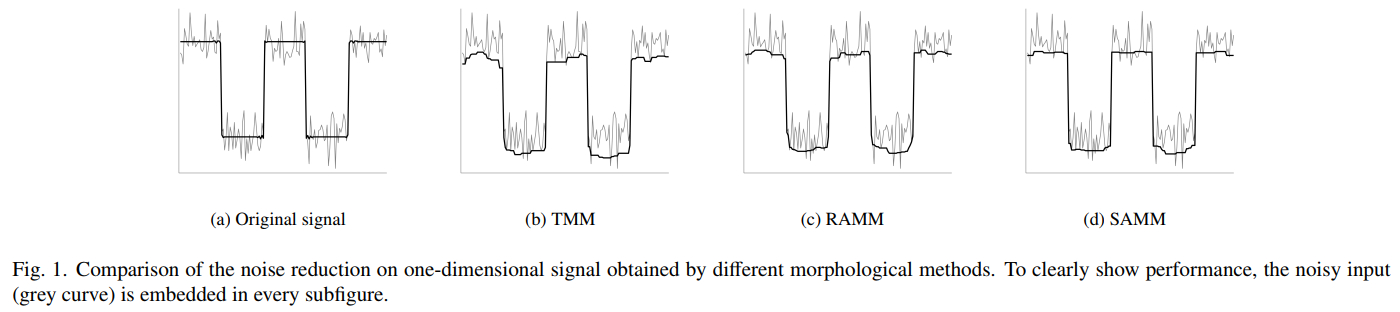
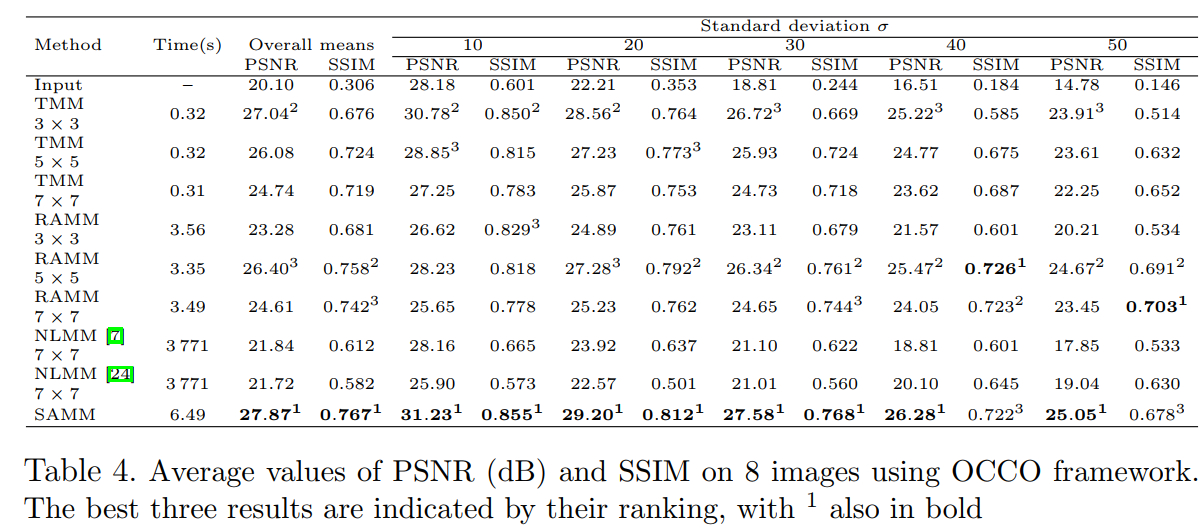
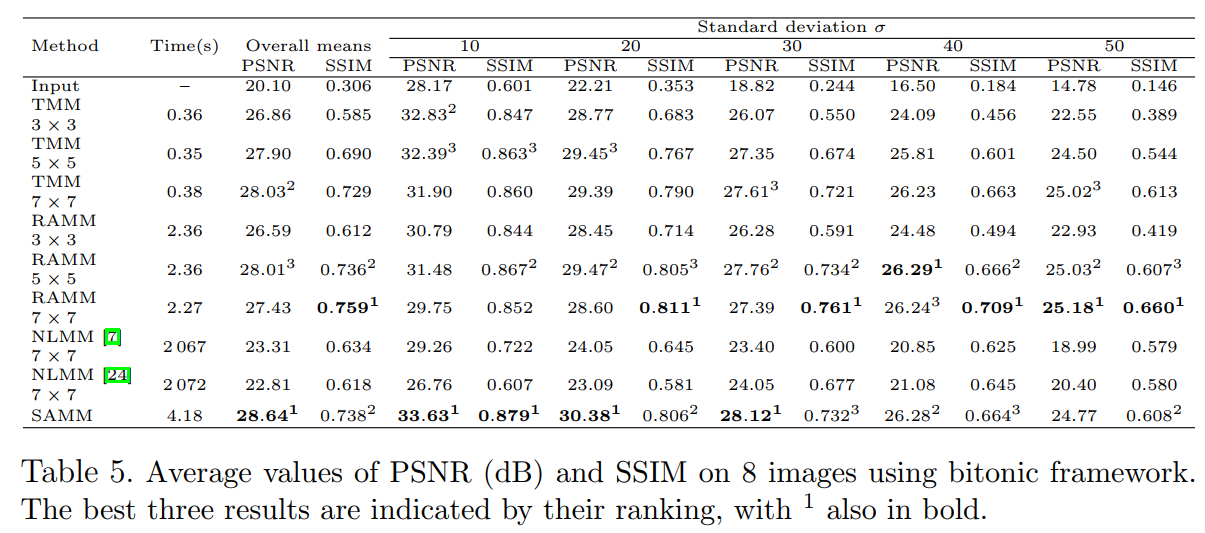
effectiveness of our SAMM both quantitatively and perceptually. In the denoising
experiments, SAMM achieves the best performance in the nine algorithms involved,
with its PSNR value surpassing the second-ranked approach by more than 0.6 dB
overall. Additionally, its SSIM quantification metric also ranks prominently
among the top performers.
Paper and Code
M. Zhang, M. Sun, H. Sun, Z. Sun*. Adaptive Mathematical Morphology with Fuzzy Structuring Element. Computing and Informatics (CAI), vol. 42, no.2, pp. 317-342, 2024. code
Algorithm



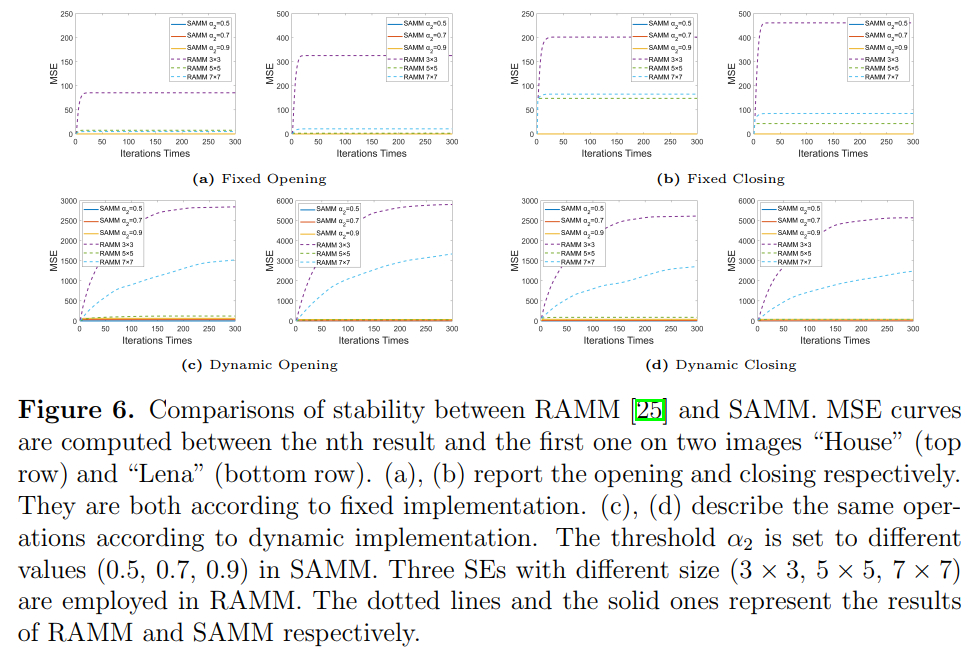
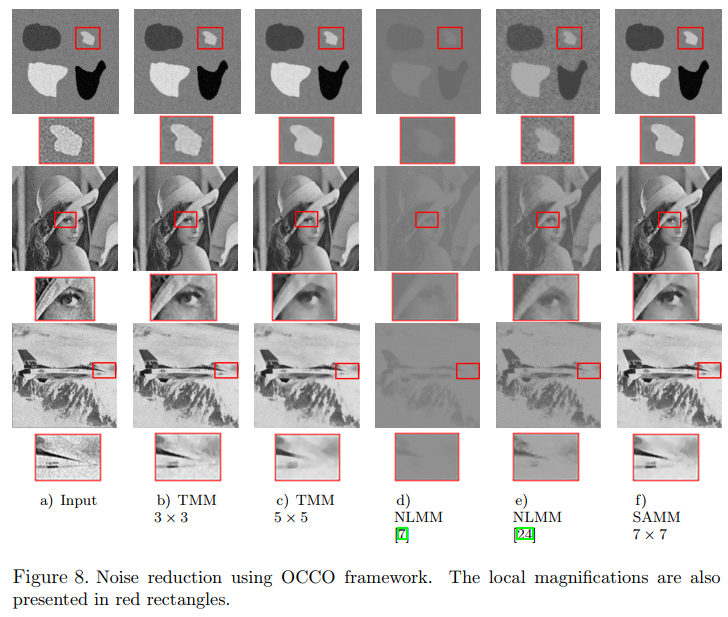
Visualization Results



Theories